向量数据库(一)
写在前面
最近在学习一些 AI 相关的开发,了解了一些未接触过的东西,其中有一部分是向量数据库,想开一个专题,对相关的内容做一下整理。
内容
什么是向量数据库
一般在我们的日常开发中,使用的数据库存储主要有两种形式:行存储形式和列存储形式。
行存储形式常见的就是我们的 MySQL,列存储形式常见的有 HBase。
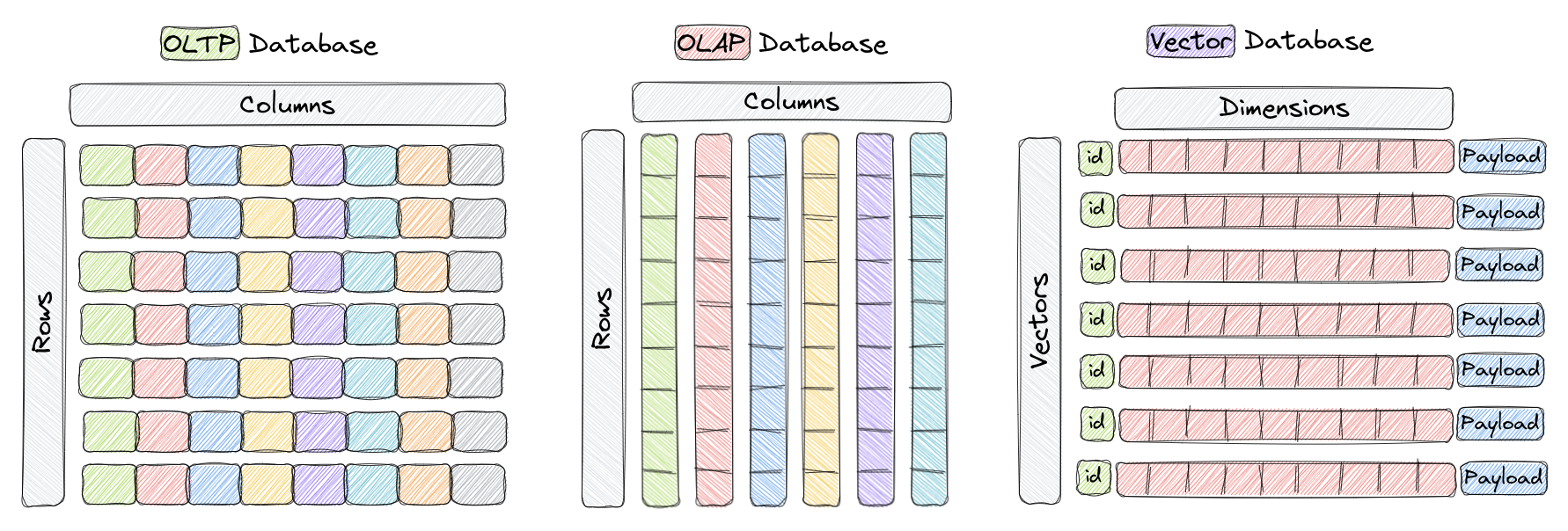
数据用行存储和列存储有什么区别呢?
假设有一个用户信息表,如果用行存储,在磁盘里的表现形式是:
| 0xa01 | 0xa02 | 0xa03 | 0xa04 | 0xa05 | 0xa06 |
|---|---|---|---|---|---|
| 张三 | 18 | 男 | 李四 | 19 | 男 |
而如果是用列存储,则相同属性的数据,会靠在一起:
| 0xa01 | 0xa02 | 0xa03 | 0xa04 | 0xa05 | 0xa06 |
|---|---|---|---|---|---|
| 张三 | 李四 | 18 | 19 | 男 | 男 |
我们可以发现,假如我想查询某个用户的数据,那么对于行存储,我只要找到张三,然后顺序遍历下去,就可以拿到该用户的全部记录了。而如果是列存储,则为了组装出这个用户的数据,需要跳过多个内容才能获取到。
但如果我想统计有多少个男性这样的数据,行存储则反过来需要全表遍历了。而列存储我只需要找到性别列的开头位置,然后顺序遍历下去,统计即可。
于是行存储和列存储就引申出了两类数据处理:OLTP 和 OLAP。
OLTP(Online transaction processing)翻译为联机事务处理,是关系型数据库的主要应用,常用来做数据的查询,也就是我们的 Select 操作(想想对于关系型数据库,我们经常提到的就是如何优化查询语句之类的问题)。
OLAP(OnLine Analytical Processing)翻译为联机分析处理,则是常用来做分析、决策的操作,例如 Group By 之类的操作。
所以日常生活中,我们需要根据实际的业务情况,考虑这块业务是倾向于事务处理,还是分析处理,然后再反推回我们需要怎样的数据库。
但随着人工智能的发展,有些数据需要以更高维度的形式存在,例如图像识别、推荐系统等,它们用到了数学上的向量来进行表示。而行存储和列存储,都是从二维的角度来处理,也就是传统的数据库是难以很好地处理更高维度的数据,因此就有了向量数据库。
在向量数据库里,一个向量就是一条数据,例如一张图片,一只狗。一个向量里会有多个元素,代表着这个事物的多个特征,假设说我们想要从毛发、鼻子长度、体型、颜色的四个维度来标识一只狗,那么这个向量里就要有这四个元素。
由于我们可以用多个维度来标识一个事物,也就意味着如果我们想要知道事物之间的关系,有了更多的条件来让我们判断。利用数学上向量的某些距离度量算法,就可以让我们实现这个目标。举个例子,假设我们有四个向量,向量A-人物小A、向量B-人物小B、向量C-猫和向量D-老鼠。如果我们从物种维度上来进行距离度量,则小A和小B的距离应该是小于小A和猫的距离,毕竟物种不同。从另外一个角度,假设小A是警察,小B是贼,我们可能通过计算发现,小A和小B之间的距离,居然跟猫和老鼠之间的距离差不多,这种情况可能就容易让我们产生一种类比的关系。所以用多维向量来表示事物,让我们有了更多的想象空间。
向量的距离度量
向量之间的距离度量,一般有三种方法:
- 余弦相似度
- 点积
- 欧几里得距离
余弦相似度
余弦相似度就是我们高中数学的时候,会计算的 cos 的值。如果两个向量方向相同,cos 等于1,如果方向相反,cos 等于 -1。我们可以通过之间的夹角大小,来判断这两个向量之间的关系大小。
余弦相似度主要应用于文本信息检索领域。因为它只关注向量之间夹角的大小,而不是长度(对于一篇文章来说,可能是某个词出现的频率)。因此如果单纯依靠文章的某个词出现的频率来判断文章之间的相似性,就会存在不足。于是比较文章的相似性,就是比较向量之间的方向,这个方向在文章上的体现,就是关键词之间的相似性。所以就算两篇文章的长度差异很大,但如果主题鲜明,关键词相似,就很容易被算出来有极大的相似性。
进一步来说,余弦相似度常用于高维稀疏向量。而文章向量化后,也往往是这种向量。高维在文章的体现就是一篇文章里有不同的多个词,每个词是一个维度;稀疏指的是虽然一篇文章里有多个词,但他们在整个大的词库里,又是小部分的存在。
我们使用余弦相似度来比较文章的相似性,意味着我们是在比较它们在语义和词汇使用模式上的相似性,而不受文章长度或具体词频的绝对值影响。
点积
点积是将两个向量之间各自的值相乘,然后将乘积相加,最终得到一个数值。我们通过这个总和的大小,来判断这两个向量之间关系的大小。
与余弦相似度的忽略向量长度相比,点积不直接考虑向量的方向,而是考虑向量的长度。例如在推荐系统里,使用点积来计算用户对物品的偏好强烈程度,就会使用到点积,因为最后会得出一个数值,这个数值往往可以用来衡量用户对某种物品的喜爱程度。
其实也比较好理解,同样都是文章,我们倾向于比较相关性,就关系到向量的夹角(方向),那就使用余弦相似度;对于两个不同的东西,我们可能倾向于比较得分、强度等,使用点积就更为合理。
欧几里得距离
欧几里得距离,则是计算两个向量的顶点之间的距离,通过顶点距离的大小来判断两个向量之间关系的大小。
欧几里得距离的直观的几何意义,让它自然而然地在对于空间几何在距离的问题上,有很好的应用。